Transformer - Attention Is All You Need 논문 한글 번역

 Attention Is All You Need논문을 직역 및 의역으로 작성한 내용입니다.

Abstract

Dominant sequence transduction mode은 encoder와 decoder를 가지고 있는 complex recurrent or convolutional neural network 구조로 되었습니다. 최고의 성능 모델 역시 attention mechanism을 이용한 encoder and decoder로 연결되어 있습니다. 오직 attention mechanism으로 구성된 간단한 구조 Transformer를 제안합니다(recurrence and convolution은 제외함). 두 기계번역의 실험은 병렬처리와 훈련 시간 감소되면서 더 좋은 품질을 냈습니다.

 

1. Introduction

Recurrent neural networks, long short-term memory and gated recurrent neural networks는 SOTA(state of the art) Language modeling and machine translation과 같은 sequence modeling and transduction problems에서 성과를 많이 이루었다.

많은 노력이 recurrent and machine translation과 같은 sequence modeling and transduction problems에서 성과를 많이 이루었으며, 많은 노력이 recurrent language models and encoder-decoder architectures로 계속 노력 중이다.

Recurrent models input and output sequences의 위치에 따라 계산을 한다. 연산 steps의 위치에 따라, 이전 hidden state h_t-1 과 position t 의 input 그들은 hidden state h_t가 생성된다. 이런 inherently한 sequential 본질을 병렬처리를 못 하게하며, 이런 특징은 긴 문장에서는 critical한 문제이다. 메모리 제약으로 인해 예제에서 일괄 처리가 제한됨.

최근 연구에서 factorization tricks과 conditional computation을 통해 연산 효율이 상당히 증가하고 또한 model performance도 좋아졌지만, 여전히 fundamental constraint of sequential은 남아있다.

Attention mechanism은 많은 분야에서 compelling sequence modeling and transduction model 필수적인 부분이 되었다.  Input or output sequence의 거리의 제약을 받지 않게 하였다.

하지만 몇 가지 경우를 제외하고 attention mechanism은 recurrent network를 사용하다.

Transformer architecture는 input and output사이의 dependencies를 설계하기 위해 recurrence를 사용하지 않는다. 대신 attention mechanism만 사용한다. Transformer는 병렬처리가 가능하고 번역 품질에서 SOTA를 이루었다.

 

2. Background

Sequential computation 감소의 목표는 Extended Neural GPU, ByteNet, ConvS2S를 기초로 형성했다.

 

3. Model Architecture

The Transformer - model architecture.

가장 경쟁적 있는 neural sequence transduction models은 encoder-decoder 구조를 이용한다. 그래서 encoder는 input sequence(x₁, …, x_n) 을 continuous representations z = (z₁, …, z_n) 에 mapping된다. 주어진 z으로, output sequence (y₁, …, y_n)  이 생성된다.

각 step은 Input data와 이전에 생성된 symbols를 사용하는(input data + hidden state) auto-regressive이다. 

Transformer의 전체적인 architecture는 encoder와 decoder에 stacked self-attention, point-wise, fully connected layers 을 사용한다. left(encoder), right(decoder)

3.1 Encoder and Decoder Stacks

Encoder는 N=6개의 layers가 쌓여있습니다. 그리고 두 개의 sub-layers를 가지고 있다.

1. multi-head self-attention mechanism
2. position-wise fully connected feed-forward network
3. layer normalization에 따라, 두 sub-layers에 residual connection
4. input and output of dimension은 d_model=512

Decoder도 역시 N=6개의 layers가 쌓여있습니다. 그리고 세 개의 sub-layer를 가지고 잇습니다.

1. multi-head self-attention mechanism
2. layer normalization에 따라, 두 sub-layers에 residual connection
3. subsequent positions 추가로 부터 prevent positions를 위해 decoder stack에 self-attention sub-layer 를 수정한다. 이를 위해 사용되는 방법이 Masking이다. output embeddings과 결합된 것은 one position…. offset이다. Position i를 예측은 오직 i 보다 작은 위치, 알려진 outputs(왼쪽)에 의해서만 예측된다.

3.2 Attention

Attention function은 vector query와 vector key-value쌍을 output에 mapping하는 것입니다. Output은 각 values의 weighted sum으로 계산되고, 각 value의 weight는 key와 query의 compatibility function에 의해 계산됩니다.

3.2.1 Scaled Dot-Product Attention

(left) Scaled Dot-Product Attention. (right) Multi-Head Attention consists of several attention layers running in parallel.

 

Input은 query와 d_k 차원의 keys과 d_v 차원의 values로 구성된다.

dot-product 계산법

values의 weight를 구하기 위해 query와 all key를 곱하고 d_k 를 각각 나누고 softmax 함수를 적용한다. 실제, Matrix Q로 변환해서 queries set를 동시에 attention function을 계산한다. Keys와 values 역시 matrices K와 V로 계산한다.

softmax를 적용하기 전 작은 gradients를 가지기 위해 1/√d_k 을 곱해서 dot product을 조정한다.

(논문에서는 dot products는 크기를 키우고, 큰 dk 는 좋지 않은 영향이 있을거라 의심하고 있다.)

3.2.2 Multi-Head Attention

h times의 querys, keys and values 를 h 개를 각각 곱한다.

병렬로 attention function을 수행하고, dv -차원의 output values를 산출한다.

Outputs을 합치고 한번 더 projected를 수행한다.

Multi-head attention을 통해 모델은 서로 다른 위치에서 다양한 표현 하위 영역의 정보를 공동으로 확인할 수 있다.

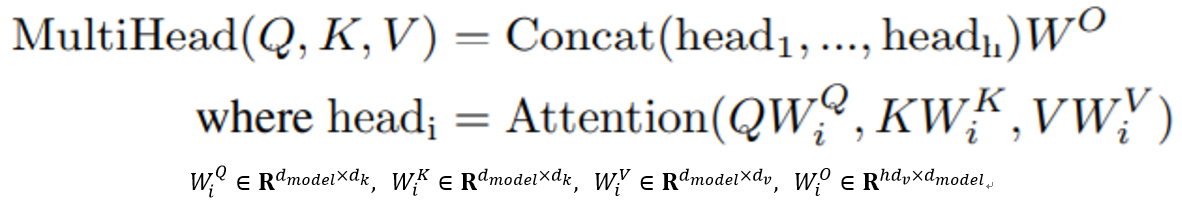
h=8로 병렬 수행하였습니다. dk=dv=dmodel/h=64 (각 헤드의 차원 줄이기 위함. 총 연산 비용은 single-head attention과 유사하다.)

3.2.3 Application of Attention in our Model

Transformer는 3가지 방법으로 multi-head attention을 사용한다.

• In “encoder-decoder attention” layer에서 query는 이전 decoder layer로부터 온다. 그리고 keys와 values는 encoder의 output로부터 온다. 이렇게 하면 decoder의 모든 position이 input sequence의 모든 position에 참석할 수 있다(전형적인 seq2seq 방식과 동일).
• encoder는 self-attention layer를 포함한다. Keys, values, querys의 모든 self-attention layer은 encoder의 이전 output으로부터 온다. encoder의 각 position은 encoder의 이전 layer에 all position에 참석할 수 있다.
• 유사한 방법으로, decoder의 self-attention layers는 decoder의 각 position에게 that position까지 decoder의 모든 position에 참석할 수 있도록 한다. auto-regressive property를 유지하기 위해 leftward information flow를 방지할 필요가 있다. scaled dot-product attention에   illegal connections로 수렴하기 위해 softmax의 input 모든 values에 masking out(setting to −∞)

3.3 Position-wise Feed-Forward Networks

추가로 각 position을 구분하기 위해 attention sub-layers, encoder and decoder의 각 layer는 fully connected feed-forward network로 구성되어 있다. 이것은 두 개의 linear transformations와 ReLU activation으로 구성되어 있다. 다른 position에서는 같은 linear transformations을 사용하지만,  다른 parameters를 사용한다.

input and output dimensionality는 d_k=512 , 그리고 inner-layer는 d_ff=2048 을 가지고 있다.

3.4 Embeddings and Softmax

다른 sequence transduction models과 유사하게, input tokens와 output tokens를 dmodel  차원의 vectors로 변환하기 위해 learned embedding을 사용한다. 우리는 decoder output을 예측 next-token probabilities로 변환하기 위해 또한 usual learned linear transformation and softmax function 사용한다. In our model에서, 두 embedding layers와 pre-softmax linear transformation 사이에 same weight matrix를 공유한다. embedding layers에서 weight dmodel 을 곱한다.

3.5 Positional Encoding

우리 model은 sequence의 order를 사용하는 recurrence와 convolution이 없기 때문에, sequence token의 relative 또는 absolute position의 대한 정보를 넣어줘야 한다.

마지막에, 우리는 input embeddings의 encoder와 decoder stacks의 bottoms에 positional encoding을 추가한다. Positional encodings는 두 개를 더하기 위해 같은 차원을  dmodel  가지고 있다.

이 작업을 위해, 우리는 sine and cosine 함수를 사용한다.

PE_(pos,2i)=sin⁡(pos/10000^2i/d_model )

PE_(pos,2i+1)=cos⁡(pos/10000^2i/d_model )

pos는 position 그리고 i는 차원이다. 이 식은, positional encoding의 각 차원은 sinusoid를 대응한다. geometric progression wavelengths의 범위는 2π부터 10000ㆍ2π까지다. 우리는 relative positions을 쉽게 배울 수 있다고 가정하기 때문에 우리는 이 함수를 사용한다. fixed offset k, 은 의 linear function표현될 수 있기 때문이다.

4. Why Self-Attention

이번 section에서는 self-attention layers와 recurrent and convolution layers를 비교한다. 비교 방법은 symbol representations(x1, ..., xn)의 one variable-length sequence를 같은 길이 (z1, ..., zn)으로 mapping 이다. 우리가 self-attetion을 사용하는 이유는 세가지이다.

첫째 layer별 총 연산의 complexity이다. 두번째는 필요한 최소 sequential operations으로 측정한 병렬처리 연산량이다.

세번째는 Network에서 long-range dependencies 사이 path length이다. long-range dependencies의 학습은 번역 업무에서 key chanllenge(핵심 도전)이다. 이러한 dependencies을 학습하는 능력에 영향을 미치는 한 가지 핵심 요소는 전달해야 하는 forward 및 backward signal의 길이입니다. input의 위치와 output의 위치의 길이가 짧을수록 dependencies 학습은 더욱 쉬워진다. 그래서 서로 다른 layer types로 구성된 네트워크에서 input과 output 위치 사이 길이가 maximum 길이를 비교한다. 

As noted in Table 1, 하나의 self-attention layer는 연속적으로 수행되는 operations 수의 모든 positions 연결한다. 반면, recurrent layer는 O(n) sequential operations이 필요하다. 즉, representation dimensionality d보다 작은 sequential length n일 때, 복잡한 연산에서 self-attention layers이 recurrent layers보다 빠르다.

Maximum path lengths, per-layer complexity and minimum number of sequential operations for different layer types. n is the sequence length, d is the representation dimension, k is the kernel size of convolutions and r the size of the neighborhood in restricted self-attention.

 

5. Training

 

6. Results

 

7. Conclusion

 

글이 도움되셨다면 공감 부탁 드립니다.

감사합니다.