[Deep Learning-딥러닝]딥러닝 정의 및 출현 배경 - 그래디언트 소실, 과적합(Over fitting), 많은 연산량

딥러닝을 간단하게 정의하면 ‘심층 신경망을 이용한 머신러닝 기법’이라고 할 수 있습니다. 심층 신경망은 은닉층이 2개 이상인 다층 신경망을 의미합니다.

딥러닝 신경망 구조

딥러닝이란 은닉층이 2개 이상으로 이루어진 신경망을 말합니다.(보통 2~3개) 다른 말로 다층/심층 신경망이라고 부릅니다. 과거에는 은닉층이 많으면 많을수록 성능이 좋다고 생각했습니다. 이론적으로 Hidden layer가 많으면 비선형이고 다차원인 결정 경계 학습법으로 수학적 모델보다 실 세계를 더욱 정교하게 표현(예측)할 수 있으며, 더 좋은 성능을 낼 수 있을 거로 생각했습니다. 하지만 현실은 그래디언트 소실, 과적합, 많은 연산과 같은 한계점을 나타내 한동안 인공지능 연구 분야가 침체기를 맞이하였습니다.

이번 포스팅은 단층 신경망의 한계를 알아보고 딥러닝이 이러한 문제를 어떤 방법으로 해결했는지 알아보겠습니다.

역전파 알고리즘은 “https://ynebula.tistory.com/24” 포스팅을 참고 바랍니다.

 

역전파 알고리즘의 한계

심층신경망에 학습 데이터를 입력하여 목적에 맞는 모델을 만듭니다. 심층 신경망의 학습 도구는 역전파(backpropagation – 1986년) 알고리즘이 이용됩니다. 단층 신경망의 한계는 역전파 알고리즘의 개발로 해결되었습니다.

은닉층이 늘어나면 더 좋은 성능을 발휘할 거라 예상했지만 은닉층을 추가하거나 은닉층의 노드를 늘려 역전파 알고리즘으로 학습시키면 오히려 성능이 더 저하되는 경우가 많았습니다. 이런 이유로 20여 년 가까이 신경망은 침체기를 가졌습니다.

2000년 중반 딥러닝 기술이 등장하면서 이런 문제점을 해결하면서 신경망은 다시 주목을 받게 됩니다.

역전파 알고리즘으로 심층 신경망을 학습시킬 때 겪는 어려움은 크게 세 가지입니다.

• 그래디언트 손실(vanishing gradient)
• 과적합
• 많은 계산량

신경망의 계층을 깊게 만들면 성능이 오히려 더 떨어지는 이유는 신경망이 제대로 학습되지 않기 때문입니다.

 

그래디언트 소실

역전파 알고리즘은 출력층의 오차를 은닉층으로 역전파 시켜 신경망을 학습시킵니다. 그래디언트 소실은 역전파 알고리즘으로 심층 신경망을 학습시키는 과정에서, 출력층에서 멀어질수록 신경망의 출력 오차가 반영되지 않는 현상을 말합니다.

오차가 앞쪽의 레이어까지 전달이 안돼 가중치가 변화가 되지 않습니다. 즉 학습되지 않는 현상입니다. 은닉층의 추가해서 오히려 학습에 역효과를 주게 됩니다.

딥러닝은 그래디언트 소실의 해결책으로 활성함수를 Sigmoid에서 ReLU(Rectified Linear Unit)로 변경했습니다. ReLU는 Sigmoid 보다 오차가 훨씬 더 잘 전달됩니다. 다음은 ReLU 함수의 공식입니다.

Formula - ReLU

다음 그림은 ReLU 함수의 그래프입니다. 입력이 음수이면 0을 출력하고, 양수이면 입력값 그대로 출력하는 함수입니다.

ReLU function

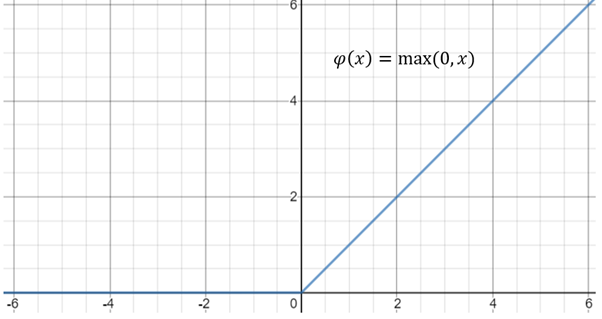
Sigmoid함수의 경우에는 입력값이 아무리 커도 신경망 노드의 출력은 1을 넘지 못했습니다. ReLU 함수는 이런 제한이 없습니다.

ReLU함수의 역전파 알고리즘을 구현하려면 ReLU함수의 도함수가 필요합니다. ReLU 함수의 도함수는 ReLU 함수의 정의에 따라 다음과 같이 주어집니다.

Formula - ReLU differential

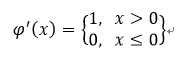
이 밖에도 Cross Entropy 함수로부터 유도된 학습 규칙을 사용하면 신경망의 학습 성능을 높일 수 있습니다. 아울러 수치 해석적으로 최적값을 더 잘 찾도록 고안된 경사하강 기법 등도 딥러닝 학습에 도움이 된다고 합니다.(sebastianruder.com/optimizing-gradient-descent)

 

과적합 – Over fitting

심층 신경망이 과적합 문제에 더 취약한 이유는 은닉층이 늘어나면 연결 가중치도 많아져 더 복잡한 모델이 되기 때문입니다. 신경망의 성능을 높이려면 은닉층을 늘려 계층 구조를 더 깊게 해야 하는데, 머신러닝의 난제인 과적합 문제에는 더 취약해지는 딜레마에 빠지게 됩니다.

은닉층이 늘어나면 연결 가중치가 높아지면서 과적합 문제가 더 취약해졌습니다.

드롭아웃(Dropout)

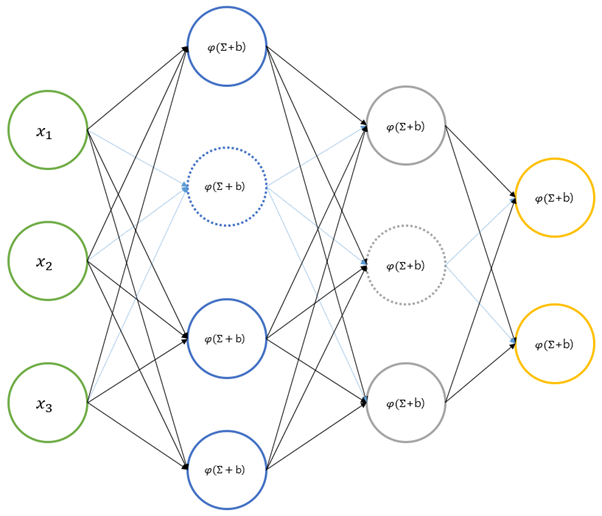
딥러닝은 드롭아웃(Dropout)을 이용해 과적합 문제를 해결했습니다. 드롭아웃은 신경망의 노드 중 무작위로 일부를 비활성화(출력을 0으로 만듦)시켜 연산에서 제외합니다. 비활성화되는 노드는 학습 때 마다 달라져, 신경망이 과적합에 빠지는 걸 효과적으로 예방할 수 있습니다. 드롭아웃의 비율은 은닉층의 경우는 50% 정도이고, 입력 노드에 적용하는 경우에는 25% 정도가 일반적입니다.

드롭아웃 훈련  - 1

드롭아웃 훈련  - 2

Regularization – 정칙화

Regularization은 모델을 단순하게 만들어 과적합을 예방하려는 방법입니다. Regularization은 비용함수에 가중치의 크기를 모두 더한 것으로 수식은 다음과 같습니다.

Formula - Regularization

λ 은 비용함수에 연결 가중치의 크기를 얼마나 반영할지를 결정하는 값입니다. 오차가 0이라도 가중치의 값이 크면 비용함수는 큰 값을 갖게 됩니다. 따라서 가중치의 크기도 되도록 작아야 합니다. 그런데 어떤 가중치의 값이 작으면 해당 노드 사이의 연결은 끊긴 것과 마찬가지가 됩니다. 결국 불필요한 노드 사이의 연결이 없어져 신경망은 더 간단한 형태가 됩니다. 또한 가중치의 크기를 작게 하면 신경망의 과적합 문제를 개선하는데 도움이 됩니다.

많은 학습 데이터

또한 대량의 학습 데이터 사용도 과적합 방지에 큰 도움이 됩니다. 학습 데이터가 많으면 그만큼 신경망이 특정 데이터에 의해 편향될 여지가 줄어들기 때문입니다.

 

많은 계산량

은닉층이 많을수록 연결 가중치가 기하급수적으로 늘어나고 학습 데이터도 많이 필요해 계산량이 급증합니다. 학습 소요 시간 문제는 GPU 같은 고성능 하드웨어의 등장과 배치 정규화(batch normalization) 등 여러 알고리즘 덕분에 상당 부분 개선되었습니다.

 

지금까지 소개한 이러한 작은 개선들이 딥러닝을 머신러닝의 총아로 등장하게 한 원동력입니다. 딥러닝의 등장으로 복잡한 비선형 모델의 구현이 가능해졌습니다.

흔히들 머신러닝의 3대 연구 분야로 영상인식, 음성인식, 자연어처리를 꼽습니다.

 

대표적인 딥러닝

• Deep Belief Network(DBN)
• Recurrent Neural Network(RNN Cell)
• Convolutional Neural Network(CNN)
• Auto Encoder
• GANs

 

글이 도움이 되셨다면 공감 부탁 드립니다.

감사합니다.

 

[Reference]

딥러닝 첫걸음